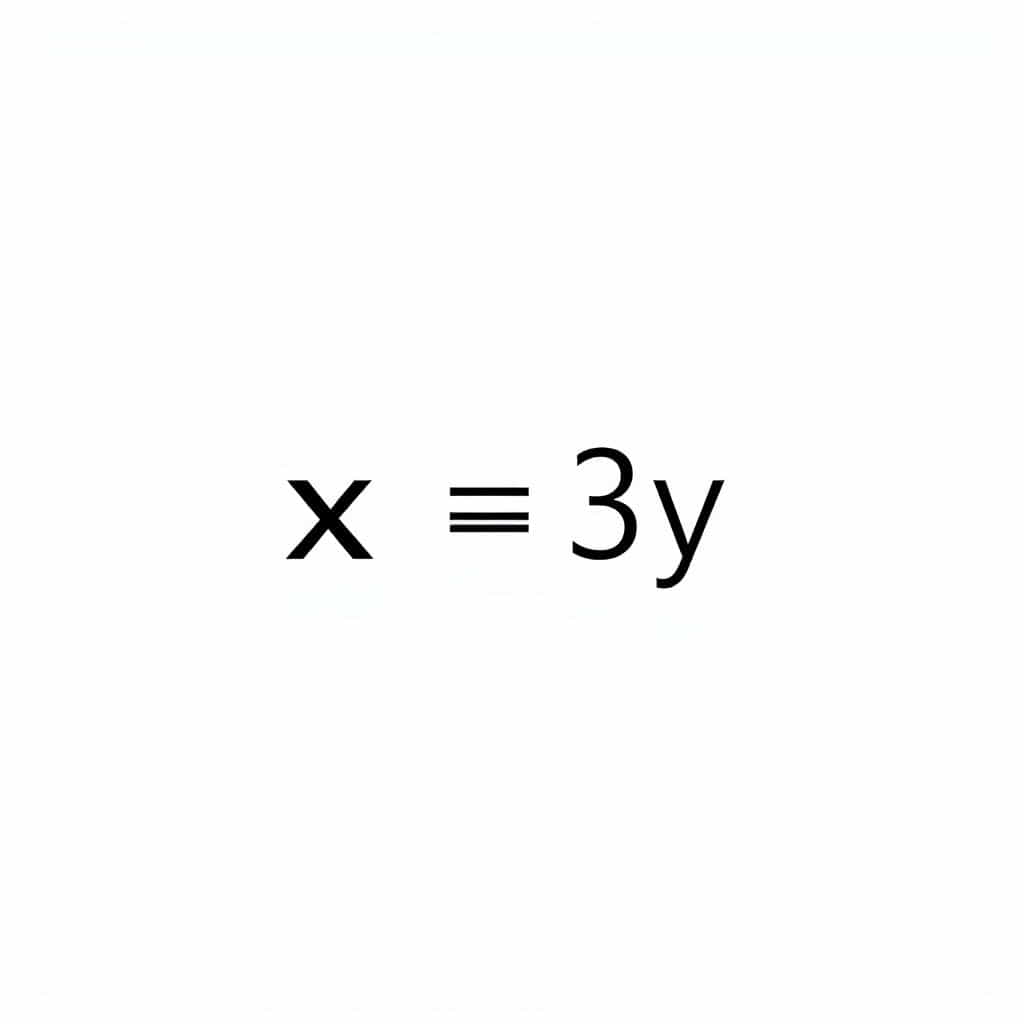Understanding the Difference of X and Thrice Y in AlgebraAlgebra is the branch of mathematics that uses symbols to represent numbers and operations. These symbols, often letters, are used to describe relationships and solve problems. One common form of algebraic expression is phrased in everyday language, such as "the difference of X and thrice Y." To understand and work with this expression, it’s important to know what each part means and how they come together in mathematical form.
Breaking Down the Expression
Let’s begin by understanding each part of the phrase
-
X This represents a variable, which is an unknown value.
-
Thrice Y This means three times the value of Y, or 3 × Y.
-
The difference of This tells us we are subtracting one quantity from another.
Putting these together, "the difference of X and thrice Y" translates to the mathematical expression
X – 3Y
What Does This Expression Represent?
In this case, X – 3Y is an algebraic expression that subtracts three times the value of Y from X. This is useful in many scenarios where you’re comparing quantities, measuring changes, or analyzing patterns.
For example
-
If X represents total income and Y represents a recurring expense that happens three times per period, then X – 3Y tells you what remains after those expenses are paid.
-
In physics, X could be total energy, and 3Y could be energy loss from three different processes.
Real-Life Applications
Understanding expressions like X – 3Y isn’t limited to math class. Here are some practical examples where this formula might come into play
1. Budgeting
Let’s say X is your salary, and Y is a regular expense (like a subscription). If you pay this subscription for three different services, then X – 3Y shows how much money you have left after paying for them.
2. Distance and Speed
Suppose you’re calculating remaining distance (X) after a vehicle slows down three times, each time decreasing distance by Y. Then X – 3Y gives the remaining stretch.
3. Resource Allocation
In project planning, if X is your total resource count and Y is the number of resources allocated to a task that happens three times, then X – 3Y reveals what’s left for other purposes.
Writing Expressions in Words and Symbols
Being able to translate between verbal and symbolic representations is a core skill in algebra. Let’s compare
| Verbal Expression | Algebraic Expression |
|---|---|
| The sum of A and B | A + B |
| The product of 4 and X | 4X |
| The difference of X and thrice Y | X – 3Y |
| Twice the difference of A and B | 2(A – B) |
| The quotient of Z and Y | Z / Y |
As seen in the table, "thrice Y" is written as 3Y, and "the difference of X and thrice Y" is written as X – 3Y.
Common Mistakes to Avoid
-
Reversing the Order Remember that "the difference of X and 3Y" means X minus 3Y, not the other way around.
-
Misinterpreting "thrice" Thrice Y means 3 times Y, not Y + Y + Y or any other operation.
-
Dropping Variables Always keep the variables in your expression unless you’re given values to substitute.
Evaluating the Expression with Real Numbers
Let’s plug in some values to see how the expression works
-
Let X = 20 and Y = 4 Then, X – 3Y = 20 – 3(4) = 20 – 12 = 8
-
Let X = 15 and Y = 5 Then, X – 3Y = 15 – 3(5) = 15 – 15 = 0
This shows how the expression changes based on the values of X and Y.
Using the Expression in Equations
Sometimes, you might need to use this expression within a larger equation. For instance
X – 3Y = 9
This equation can be solved if you know the value of one variable. For example
- If Y = 2, then X – 3(2) = 9 X – 6 = 9 X = 15
Equations like this are common in algebra and form the basis for solving real-world problems.
Graphing X – 3Y
The expression X – 3Y can also be visualized on a graph, especially when converted into an equation involving two variables. Rearranging
X = 3Y + constant
You could treat this as a linear equation and plot the relationship between X and Y. This helps in visualizing how changing Y affects X.
Building Algebraic Thinking
Learning how to understand and manipulate expressions like X – 3Y helps build strong problem-solving skills. It teaches you how to
-
Translate verbal statements into math
-
Evaluate expressions using real numbers
-
Solve equations with one or more variables
-
Recognize patterns and relationships between quantities
These skills are not only foundational in math but are also useful in science, engineering, business, and everyday life.
Summary
The phrase "the difference of X and thrice Y" is a simple yet powerful example of how algebra turns language into mathematical expressions. Written as X – 3Y, it appears in many real-world scenarios, from budgeting and planning to data analysis. Mastering how to interpret and work with such expressions is essential for building a solid understanding of mathematics.
Relevant Keywords
difference of x and thrice y, algebraic expressions, basic algebra, writing expressions in math, math translation, real-life math examples, evaluating algebraic expressions, variables and operations, understanding math language, X minus 3Y.